Predicción, clasificación y pronóstico

Clase 4

Esteban Degetau

2 de abril de 2025

Motivación

Preguntas anteriores

En clases anteriores, vimos cómo hacer inferencia sobre algunas relaciones entre variables.

• Respondimos preguntas como:

  • ¿Qué relación lineal guardan los ingresos de las personas dependiendo de su educación?

  • ¿Cuál es el efecto causal del género de una candidatura sobre su probabilidad de promoción?

  • ¿Podemos estar seguros de que estas relaciones son estadísticamente significativas?

Pregunta de investigación

En esta clase, usaremos herramientas estadísticas para responder preguntas relacionadas con predicción, clasificación y pronóstico.

• ¿Qué probabilidad tiene una persona en particular de incumplir su deuda, dependiendo sus características observables?

• Cómo puedo clasificar a una persona en grupos de riesgo (alto o bajo) de incumplimiento?

• ¿Cuántas personas incumplirán su deuda durante los próximos meses?

Tareas de predicción vs inferencia

Cuando usamos OLS para hacer inferencia, nos interesaba la relación entre dos variables.

• Decíamos que una variable independiente (\(X\)), tenía una relación sobre una variable dependiente (\(Y\)).

En tareas de predicción supervisada, seguiremos utilizando herramientas estadísticas del tipo \(Y = f(X) + \epsilon\), pero cambiaremos el lenguaje que usamos para describir el problema.

• Ahora, hablaremos de que una variable de respuesta (\(Y\)) es una función de un conjunto de variables predictoras (\(X\)).

Datos

Vamos a usar el conjunto de datos Default del paquete ISLR.

Este conjunto de datos contiene información sobre personas deudoras de tarjeta de crédito, si han incumplido o no su deuda y algunas características individuales.

pacman::p_load(ISLR, tidyverse)

data(Default)
summary(Default)

 default    student       balance           income     
 No :9667   No :7056   Min.   :   0.0   Min.   :  772  
 Yes: 333   Yes:2944   1st Qu.: 481.7   1st Qu.:21340  
                       Median : 823.6   Median :34553  
                       Mean   : 835.4   Mean   :33517  
                       3rd Qu.:1166.3   3rd Qu.:43808  
                       Max.   :2654.3   Max.   :73554  

OLS como herramienta de predicción

Modelo de probabilidad lineal

Igual que en la Clase 3, podemos ajustar un modelo de OLS para:

1. Estudiar la relación lineal entre las características de los individuos y su probabilidad de incumplimiento, y

2. Predecir la probabilidad de incumplimiento de un individuo en particular.

Relación lineal de las variables con incumplimiento

Respondamos la primera pregunta: cómo afecta cada una de las variables a la probabilidad de incumplimiento.

Para esto, ajustamos un modelo de probabilidad lineal por cada una de las variables independientes:

pacman::p_load(fixest)

Default <- Default |>
    mutate(
      default = as.numeric(default == "Yes"),
      student = as.numeric(student == "Yes")
    )

Default |>
    feols(
      default ~ sw(balance, income, student)
      ) |>
    etable(
        title = "Modelo de probabilidad lineal",
        fitstat = ~ n + r2 + my + f,
        markdown = T,
        digits = 3
    )

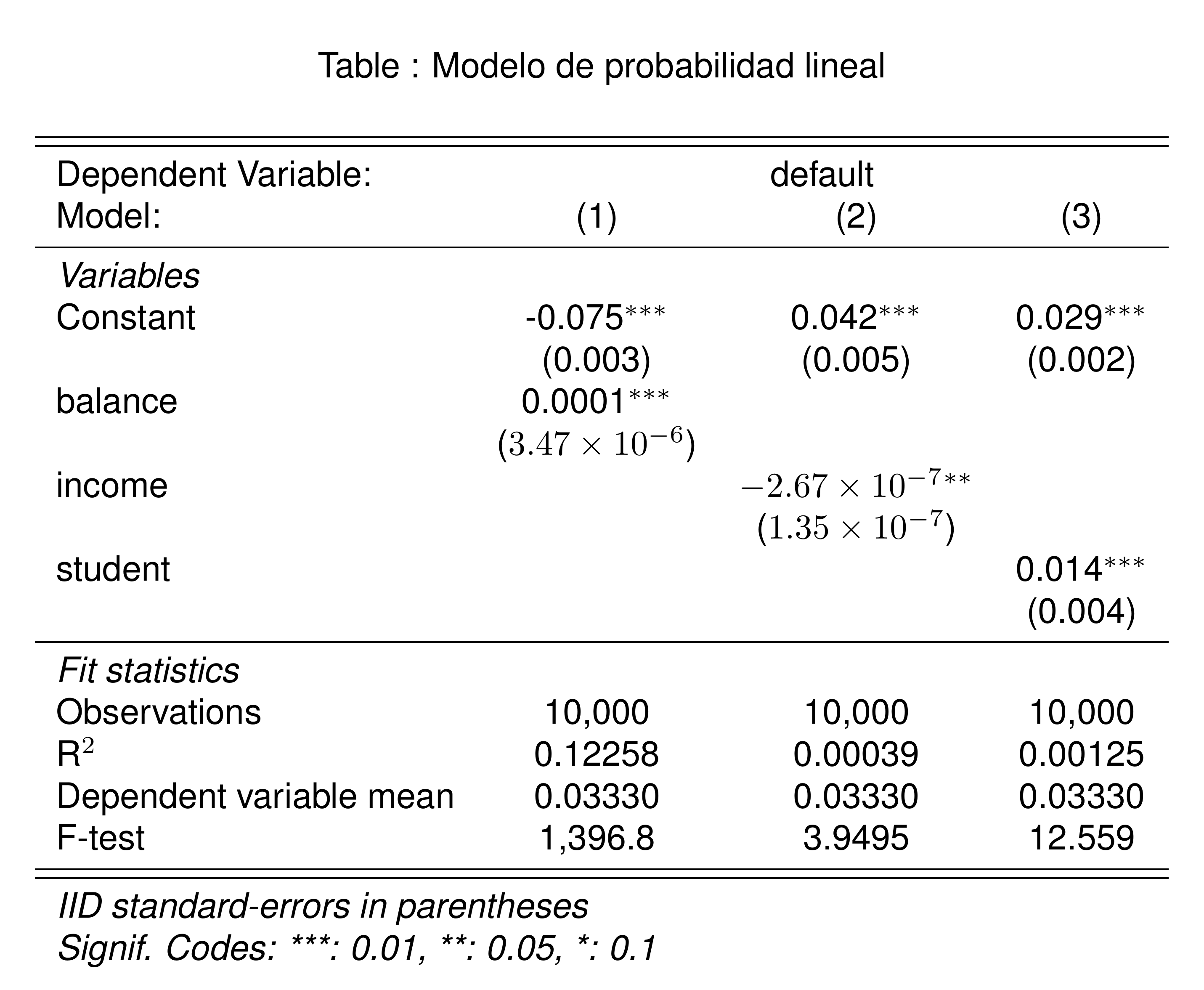
Pregunta: ¿Cómo interpretamos los resultados?

Predicción con OLS

Para modelar la probabilidad de incumplimiento con OLS, usamos la siguiente especificación:

\[ D_i = \beta_0 + \beta_1 balance_i + \beta_2 income_i + \beta_3 student_i + \epsilon_i \qquad(1)\]

Donde:

• \(D_i\) es la variable dependiente que indica si el individuo \(i\) incumplió su deuda (1) o no (0).

• \(balance_i\) es el balance de la tarjeta de crédito del individuo \(i\).

• \(income_i\) es el ingreso del individuo \(i\).

• \(student_i\) es una variable dummy que indica si el individuo \(i\) es estudiante (1) o no (0).

• \(\epsilon_i\) es el término de error.

De nuevo, el modelo descrito en la Ecuación 1 es un modelo de probabilidad lineal porque su variable dependiente es binaria.

Estimación

Estimamos el modelo de probabilidad lineal usando OLS como lo hemos hecho antes:

ols_fit <- feols(default ~ balance + income + student, data = Default)
summary(ols_fit)

OLS estimation, Dep. Var.: default
Observations: 10,000
Standard-errors: IID 
                Estimate  Std. Error  t value  Pr(>|t|)    
(Intercept) -0.081179487 0.008382077 -9.68489 < 2.2e-16 ***
balance      0.000132690 0.000003547 37.41200 < 2.2e-16 ***
income       0.000000199 0.000000192  1.03873   0.29896    
student     -0.010330101 0.005663178 -1.82408   0.06817 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 0.167925   Adj. R2: 0.123756

Aquí, no nos interesa la interpretación de los coeficientes, porque la tarea es predecir la probabilidad de incumplimiento de un individuo en particular.

Predicción

Con el modelo que estimamos, ols_fit, podemos responder la siguiente pregunta:

Ejemplo 1 ¿Cuál es la probabilidad de incumplimiento de un individuo con balance de $1000, ingreso de $50000 y que no es estudiante?

to_predict <- tibble(
  balance = 1000,
  income = 50000,
  student = 0
)

predicted_prob <- predict(ols_fit, newdata = to_predict)
predicted_prob

[1] 0.06146788

Una persona con balance de $1,000, ingreso de $50,000 y que no es estudiante tiene una probabilidad de incumplimiento de 6.15%.

Otro problema

Ejemplo 2 ¿Cuál es la probabilidad de incumplimiento de un individuo con balance de $100000, ingreso de $500 y que es estudiante?

to_predict <- tibble(
  balance = 100000,
  income = 500,
  student = 1
)

predicted_prob <- predict(ols_fit, newdata = to_predict)
predicted_prob

[1] 13.17756

Una persona con balance de $100,000, ingreso de $500 y que es estudiante tiene una probabilidad de incumplimiento de 1 317.76%.

Pregunta: ¿Qué problema tiene esta predicción?

Limitaciones de OLS

Recordemos que OLS ajusta un plano a los datos. Esto nos va a dar dos problemas para modelar probabilidades:

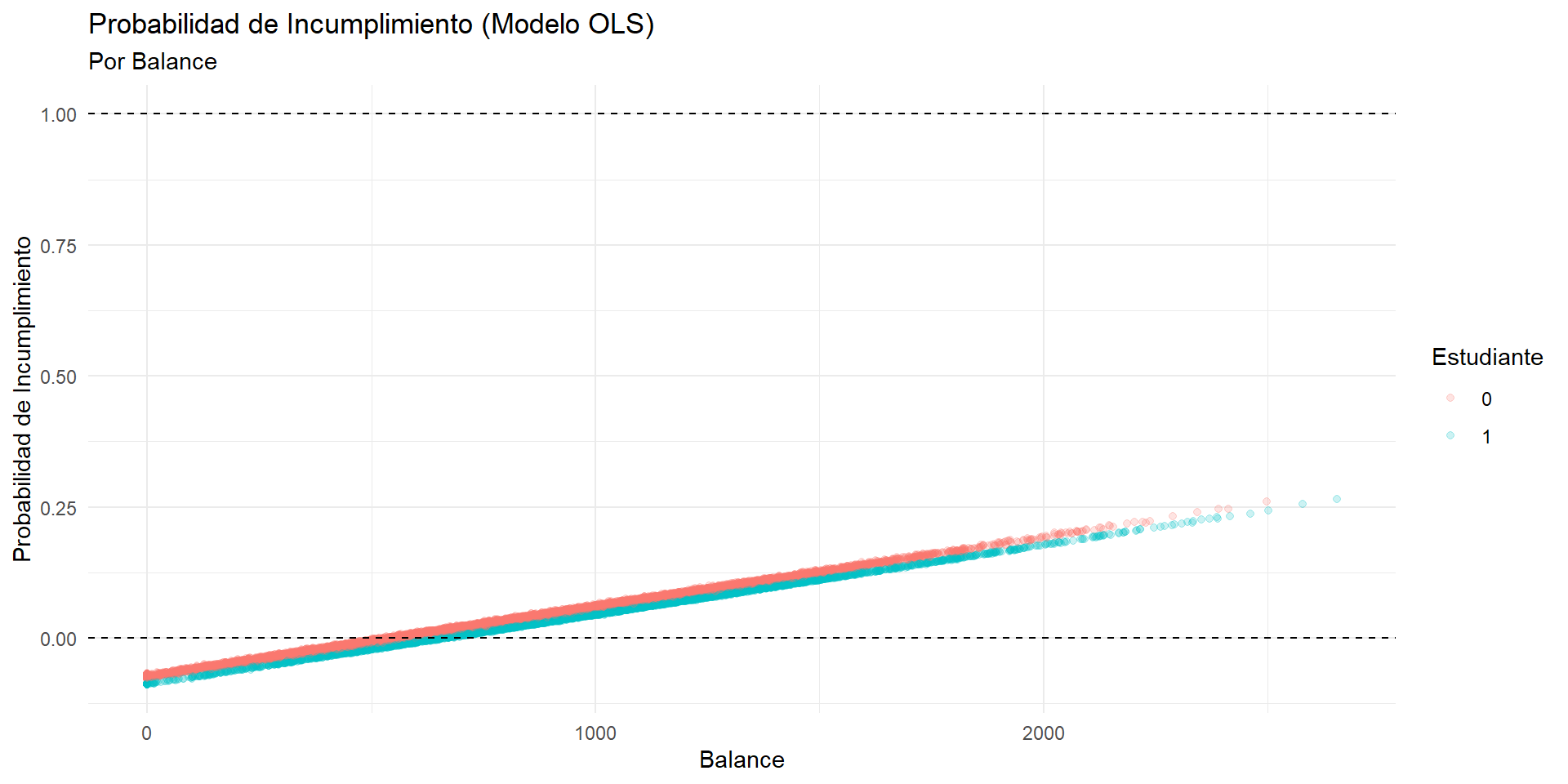
1. Predicciones fuera del rango [0, 1]: Al extrapolar, OLS puede predecir probabilidades negativas o mayores a 1.

2. Relación lineal: OLS asume que la relación entre las variables es lineal. En la realidad podemos encontrarnos con relaciones no lineales.

Visualización de la predicción

Default |>
  mutate(prob_default = predict(ols_fit)) |>
  ggplot(aes(x = balance, y = prob_default, color = as.factor(student))) +
  geom_point(alpha = 0.2) +
  geom_hline(yintercept = c(0, 1), linetype = "dashed") +
  labs(
    title = "Probabilidad de Incumplimiento (Modelo OLS)",
    subtitle = "Por Balance",
    x = "Balance",
    y = "Probabilidad de Incumplimiento",
    color = "Estudiante"
  )

Visualización de la predicción

Regresión Logística para Clasificación

Modelo Logístico

El modelo logístico o logit, viene de una familia de modelos llamados estimadores de máxima verosimilitud.

• Análogamente a OLS, que busca minimizar el error de estimación, un modelo de máxima verosimilitud (ML por sus siglas en inglés) busca encontrar los parámetros que maximizan la probabilidad de observar los datos.

• A diferencia de OLS, un ML permite incluir variables independientes que no son lineales.

• Para modelar una probabilidad, limitamos la estimación a un rango entre 0 y 1 con una función logística con regresores lineales.

Modelo Logístico

Buscamos estimar el siguiente modelo:

\[ D_i = X_i' \beta + \epsilon_i \]

Donde el término \(X_i' \beta\) es la combinación lineal de las variables independientes con sus coeficientes.

La función que acota la probabilidad entre 0 y 1 es la función logística:

\[ \mathbb P (D_i = 1 | X_i) = \Phi(X_i' \beta) = \frac{\exp(X_i' \beta)}{1 + \exp(X_i' \beta)} \qquad(2)\]

La Ecuación 2 nos permite tomar los coeficientes estimados para predecir la probabilidad de incumplimiento de un individuo, acotada entre 0 y 1.

Estimación

logit_model <- glm(default ~ ., data = Default, family = binomial)
summary(logit_model)

Call:
glm(formula = default ~ ., family = binomial, data = Default)

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -1.087e+01  4.923e-01 -22.080  < 2e-16 ***
student     -6.468e-01  2.363e-01  -2.738  0.00619 ** 
balance      5.737e-03  2.319e-04  24.738  < 2e-16 ***
income       3.033e-06  8.203e-06   0.370  0.71152    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 2920.6  on 9999  degrees of freedom
Residual deviance: 1571.5  on 9996  degrees of freedom
AIC: 1579.5

Number of Fisher Scoring iterations: 8

• Usamos la notación y ~ . para indicar que queremos usar todas las variables, además de y como predictores.

• stats::glm() es la función de base R para estimar modelos de máxima verosimilitud.

• family = binomial indica que queremos estimar un modelo logístico: que clasificaremos a los datos en dos grupos de manera supervisada.

Visualización de la predicción

Default |>
  mutate(prob_default = predict(logit_model, type = "response")) |>
  ggplot(aes(x = balance, y = prob_default, color = factor(student))) +
  geom_hline(yintercept = c(0, 1), linetype = "dashed") +
  geom_point(alpha = 0.3) +
  labs(
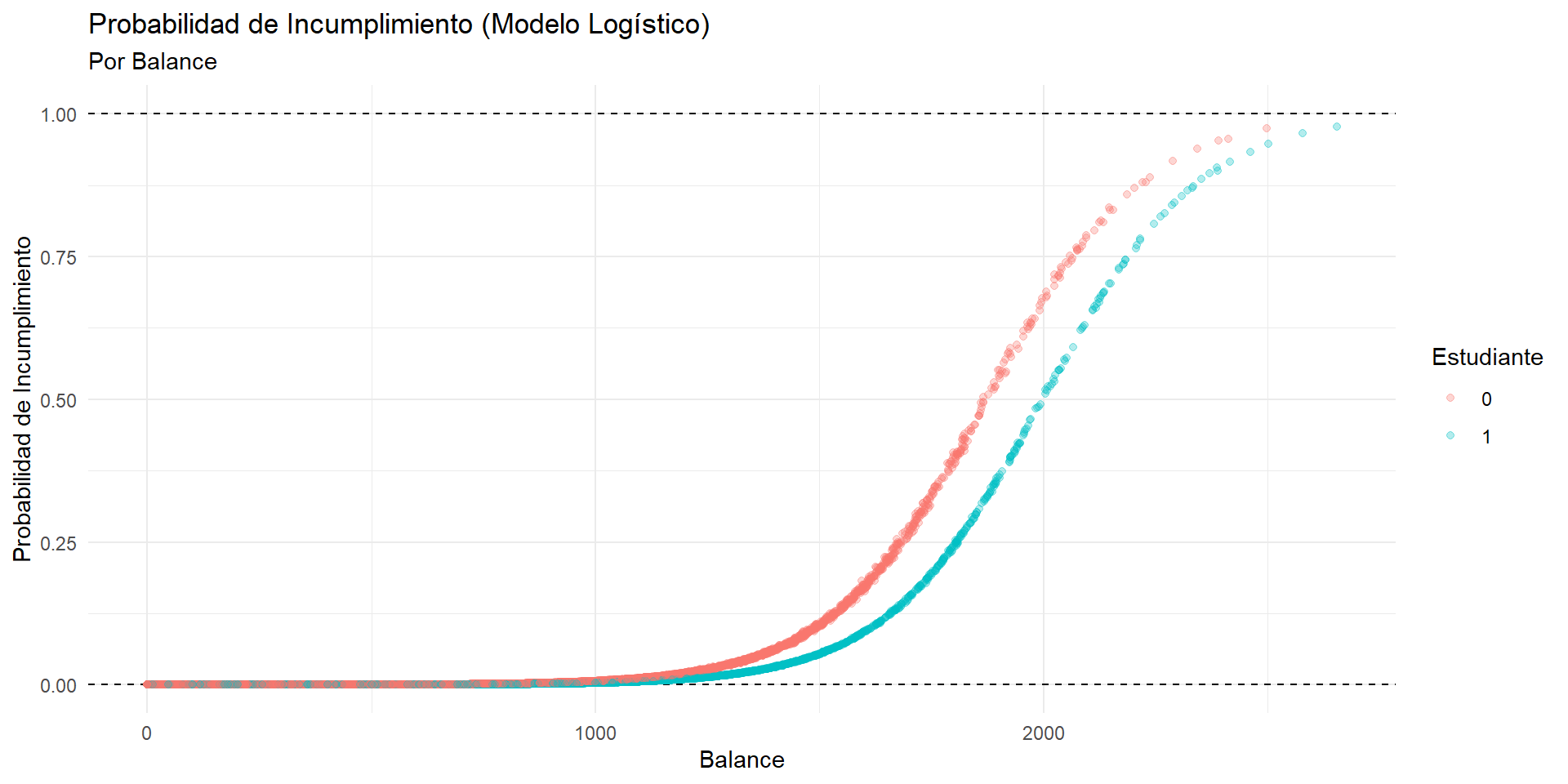
    title = "Probabilidad de Incumplimiento (Modelo Logístico)",
    subtitle = "Por Balance",
    x = "Balance",
    y = "Probabilidad de Incumplimiento",
    color = "Estudiante"
  )

Visualización de la predicción

Predicción

Para resolver los ejercicios de predicción anteriores, simplemente repetimos el procedimiento que usamos con OLS.

to_predict <- tibble(
    balance = c(1000, 100000),
    income = c(50000, 500),
    student = c(0, 1)
)


predicted_prob <- predict(logit_model, newdata = to_predict, type = "response")
predicted_prob

          1           2 
0.006821253 1.000000000 

Encontramos que las probabilidades de incumplimiento son 0.68%, 100.00% respectivamente.

Clasificación

Podemos usar el modelo logístico para clasificar a los individuos en grupos de riesgo.

• Definimos un umbral de probabilidad, por ejemplo 0.5.

• Si la probabilidad de incumplimiento es mayor a 0.5, clasificamos al individuo como de alto riesgo.

groups <- Default |>
    mutate(
        prob_default = predict(logit_model, type = "response"),
        risk = case_when(
            prob_default > 0.5 ~ "Alto",
            prob_default <= 0.5 ~ "Bajo"
        )
    ) 

Evaluación de la clasificación

Podemos evaluar la precisión del modelo (supervisado) revisando si la predicción por grupo de riesgo coincide con el estado real de incumplimiento.

• Usamos la matriz de confusión para evaluar la clasificación.

• Mediremos con qué frecuencia nuestro modelo clasifica correctamente a los individuos, dependiendo de su estado real de incumplimiento.

confusion_matrix <- table(
    groups$risk,
    groups$default
)

confusion_matrix |>
    knitr::kable()

	0	1
Alto	40	105
Bajo	9627	228

El modelo logístico clasifica muy bien a las personas que no incumplen su deuda, pero no clasifica bien a las personas que sí incumplen.

Limitaciones del modelo logístico

A pesar de que las probabilidades de incumplimiento están acotadas entre 0 y 1, el modelo logístico todavía está limitado por el supuesto de linealidad entre predictores y respuesta.

El dilema entre sesgo y varianza

Simulación

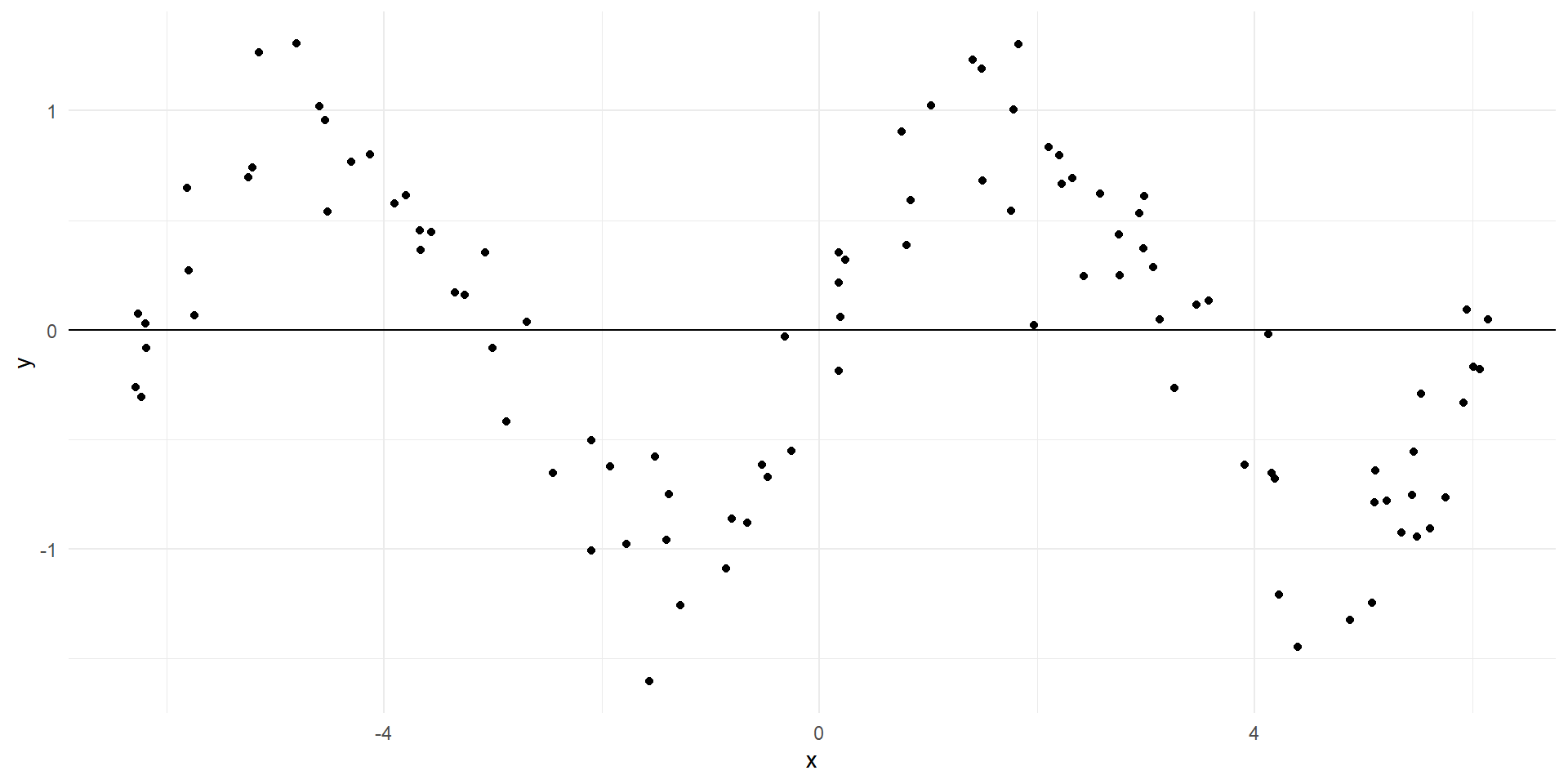
Ajuste de un modelo lineal

fit_1 <- lm(y ~ x, data = train)

train <- train |>
    mutate(
        y_hat = predict(fit_1))

train |>
    ggplot(aes(x, y)) +
    geom_point() +
    geom_line(aes(y = y_hat), color = "blue") +
    geom_hline(yintercept = 0) 

Ajuste polinomial

fit_2 <- lm(y ~ poly(x, 2, raw = TRUE), data = train)

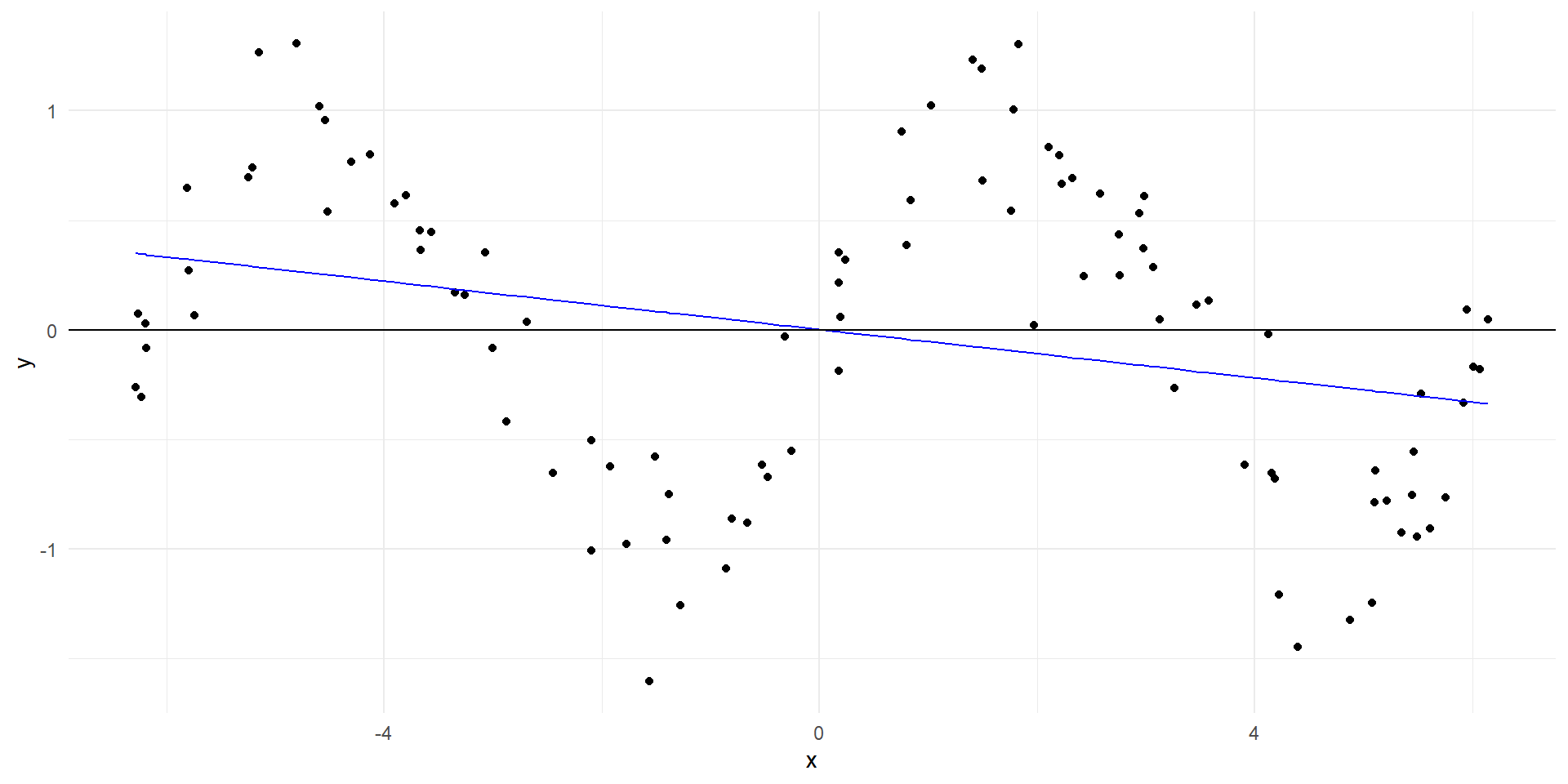
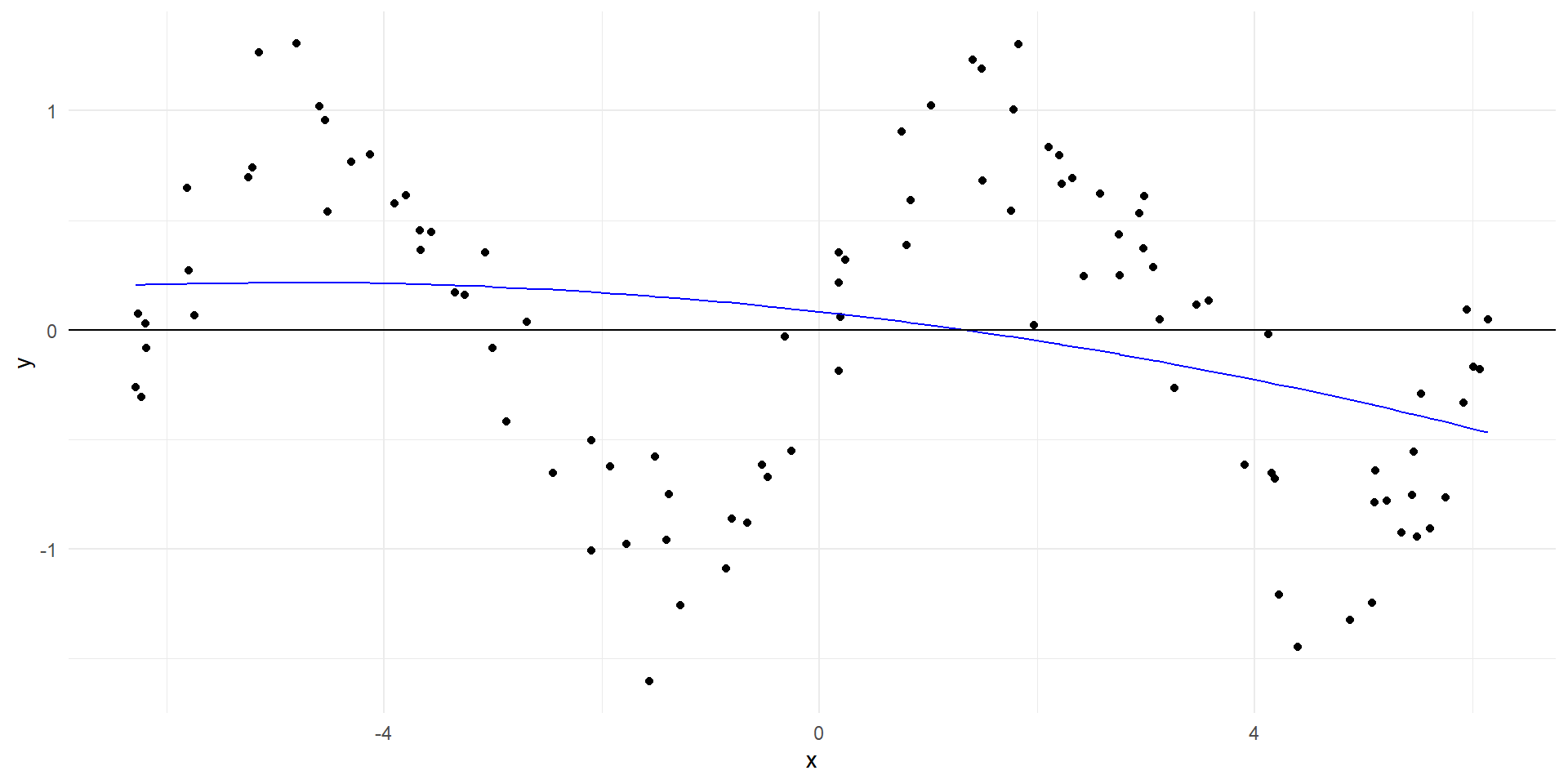
Ajuste polinomial de mayor orden

fit_3 <- lm(y ~ poly(x, 15, raw = TRUE), data = train)

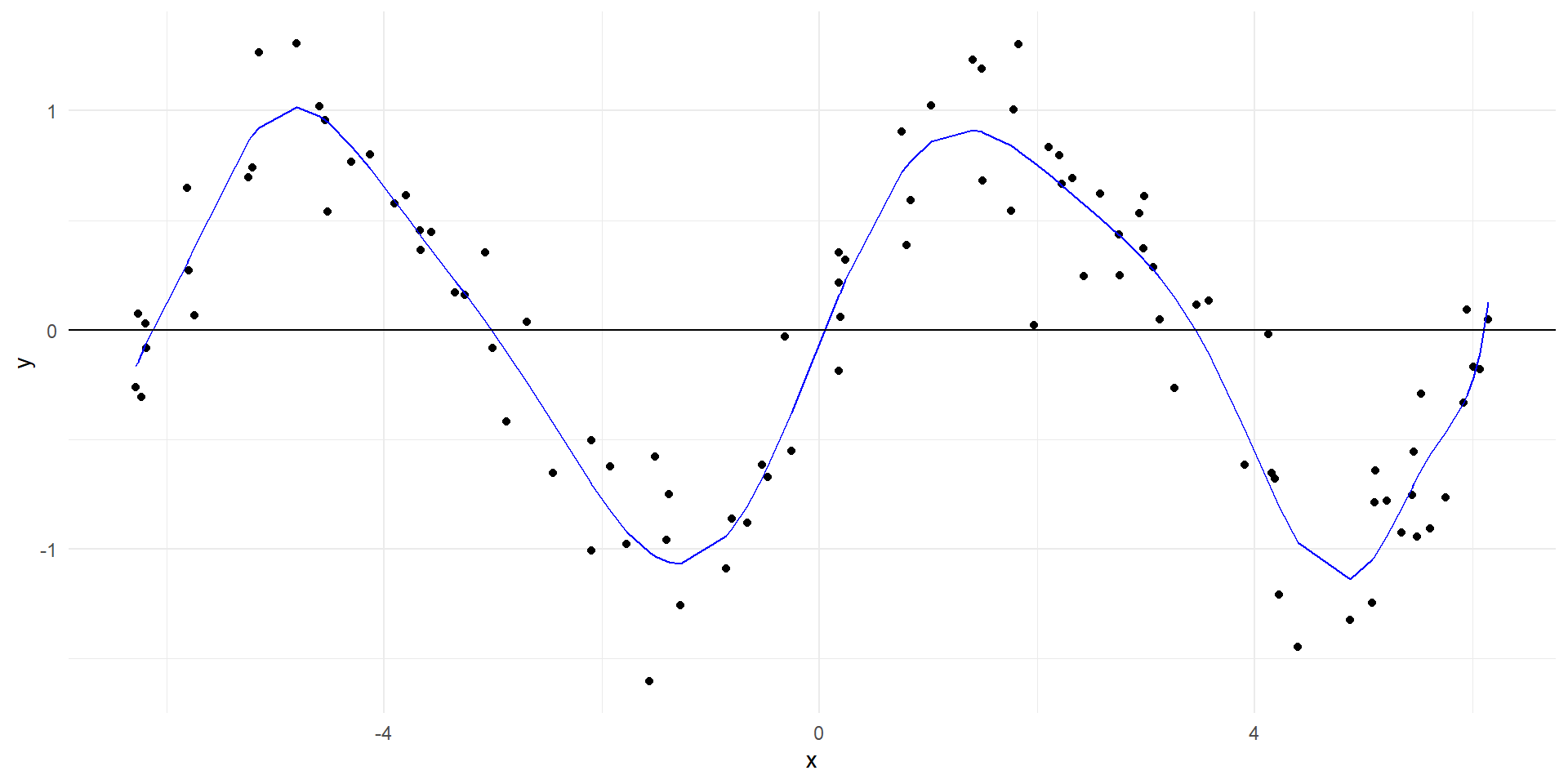
Ajuste polinomial de mayor orden

Vemos que en la medida en la que aumentamos el orden del polinomio, el modelo se ajusta mejor a los datos de entrenamiento.

Pregunta: ¿Un mejor ajuste siempre es mejor?

Evaluación de los modelos

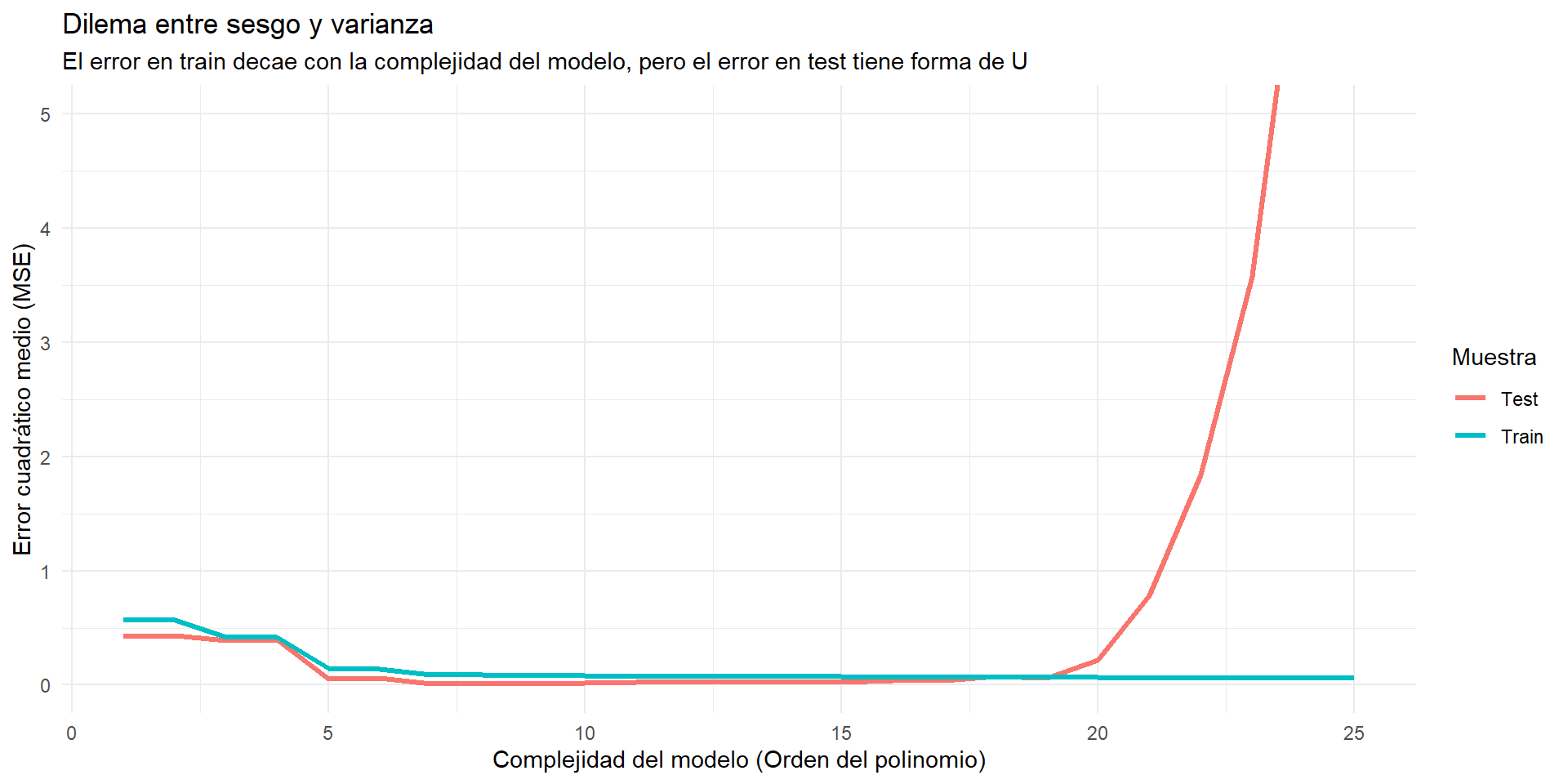
El dilema entre sesgo y varianza

Podemos tener un modelo muy complejo que se ajusta perfectamente a los datos, i.e. con un sesgo muy bajo.

• Sin embargo, al ajustarse tan bien a los datos dentro de la muestra de entrenamiento, el modelo empieza a reflejar una varianza que es idiosincrática del conjunto de entrenamiento.

• Esta varianza no se reproduce en la muestra de prueba y, por lo tanto, el modelo no generaliza bien la relación funcional entre las variables.

Error irreducible

Al dividir nuestro conjunto en dos partes, uno de entrenamiento y otro de prueba, podemos ver que el error en la muestra de prueba tiene forma de U.

• Agregar complejidad al modelo reduce el error en el conjunto de prueba, solo hasta cierto punto.

• Una vez que llegamos a un cierto nivel de complejidad, el error en la muestra de prueba empieza a aumentar.

• Los métodos automatizados de aprendizaje supervisado, como el random forest, encuentran el punto donde el error en la muestra de prueba es mínimo: encuentran el punto de equilibrio entre sesgo y varianza.

Aprendizaje no supervisado

Aprendizaje no supervisado

Hasta ahora, hemos visto cómo predecir la probabilidad de incumplimiento de un individuo en particular.

• Partimos de un conjunto de datos donde tenemos información sobre la respuesta (incumplimiento) y las variables predictoras (balance, ingreso, etc.).

• Escribimos un modelo que describe la forma funcional de la relación entre las variables predictoras y la respuesta:

  \[ D_i = f(X_i) + \epsilon_i \]

• Decimos que el aprendizaje es supervisado porque hemos observado respuestas con las que podemos entrenar y probar el modelo

Aprendizaje supervizado vs no supervisado

Ahora volteamos a procedimientos de aprendizaje no supervisado:

• No hay una respuesta observada.

• Solo tenemos un conjunto de datos con variables predictoras \(X\).

• Buscamos patrones en los datos.

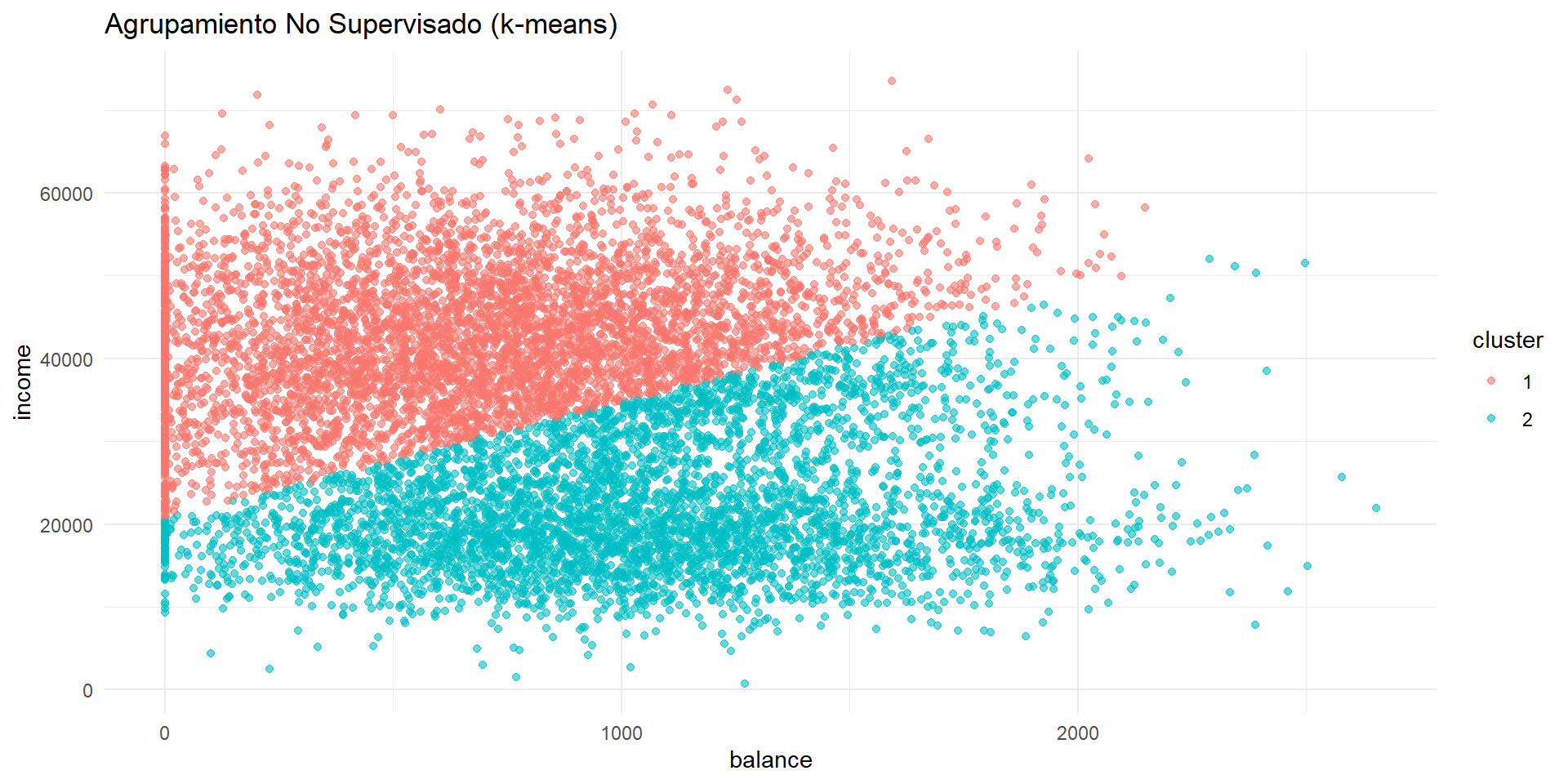
Agrupamiento por k-means

set.seed(1)
kmeans_result <- Default |>
  select(balance, income) |>
  scale() |>
  kmeans(centers = 2)

Default |>
  mutate(cluster = factor(kmeans_result$cluster)) |>
  ggplot(aes(balance, income, color = cluster)) +
  geom_point(alpha = 0.6) +
  labs(title = "Agrupamiento No Supervisado (k-means)")

Random Forest

Random Forest

Un árbol

pacman::p_load(rpart, rpart.plot)

data(Default)

set.seed(42)
tree_model <- rpart(default ~ ., data = Default)

rpart.plot(tree_model)

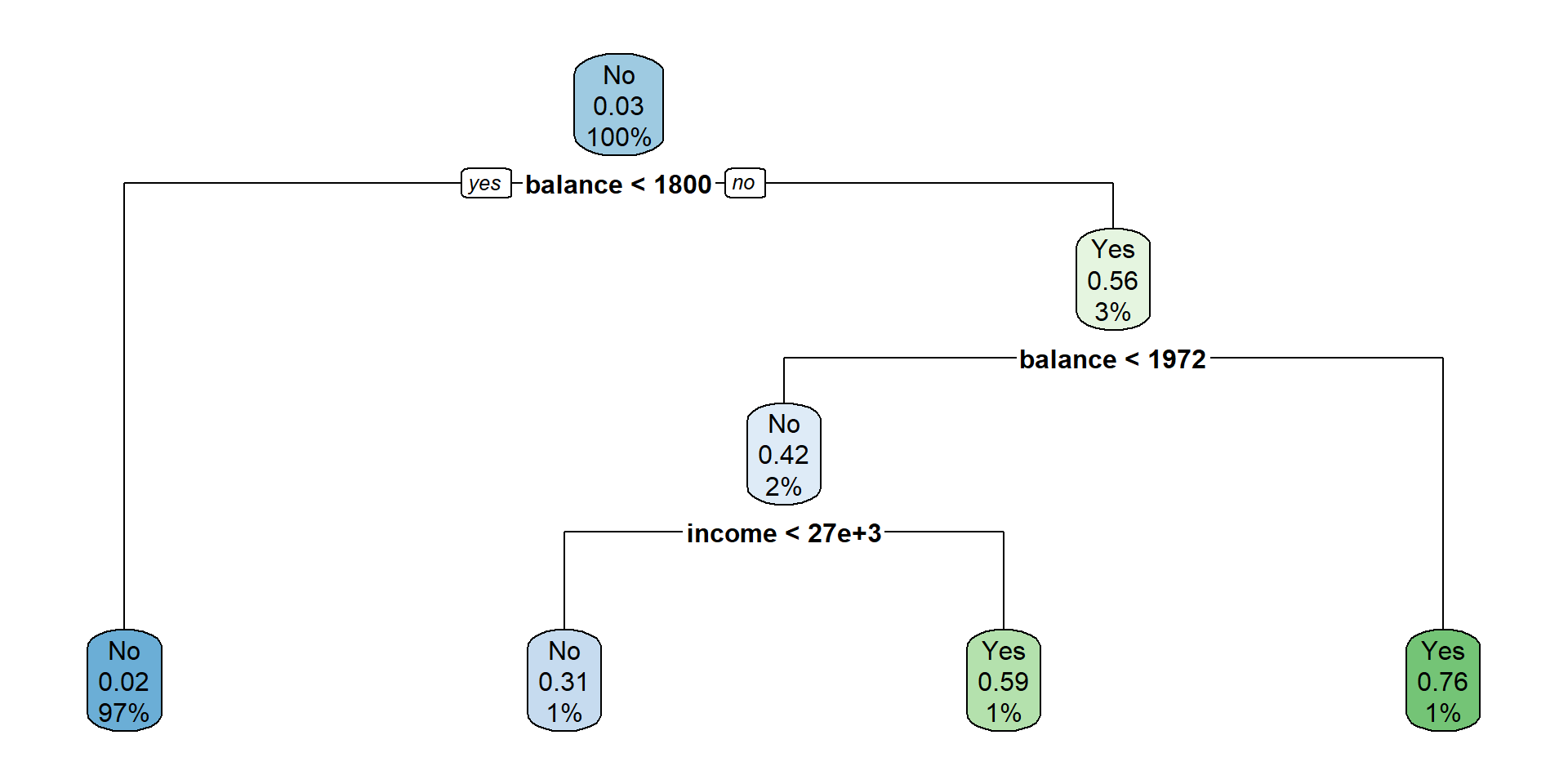
El bosque

pacman::p_load(randomForest)

rf_fit <- randomForest(
  default ~ .,
  data = Default,
  importance = T,
  ntree = 1000
) 

rf_fit

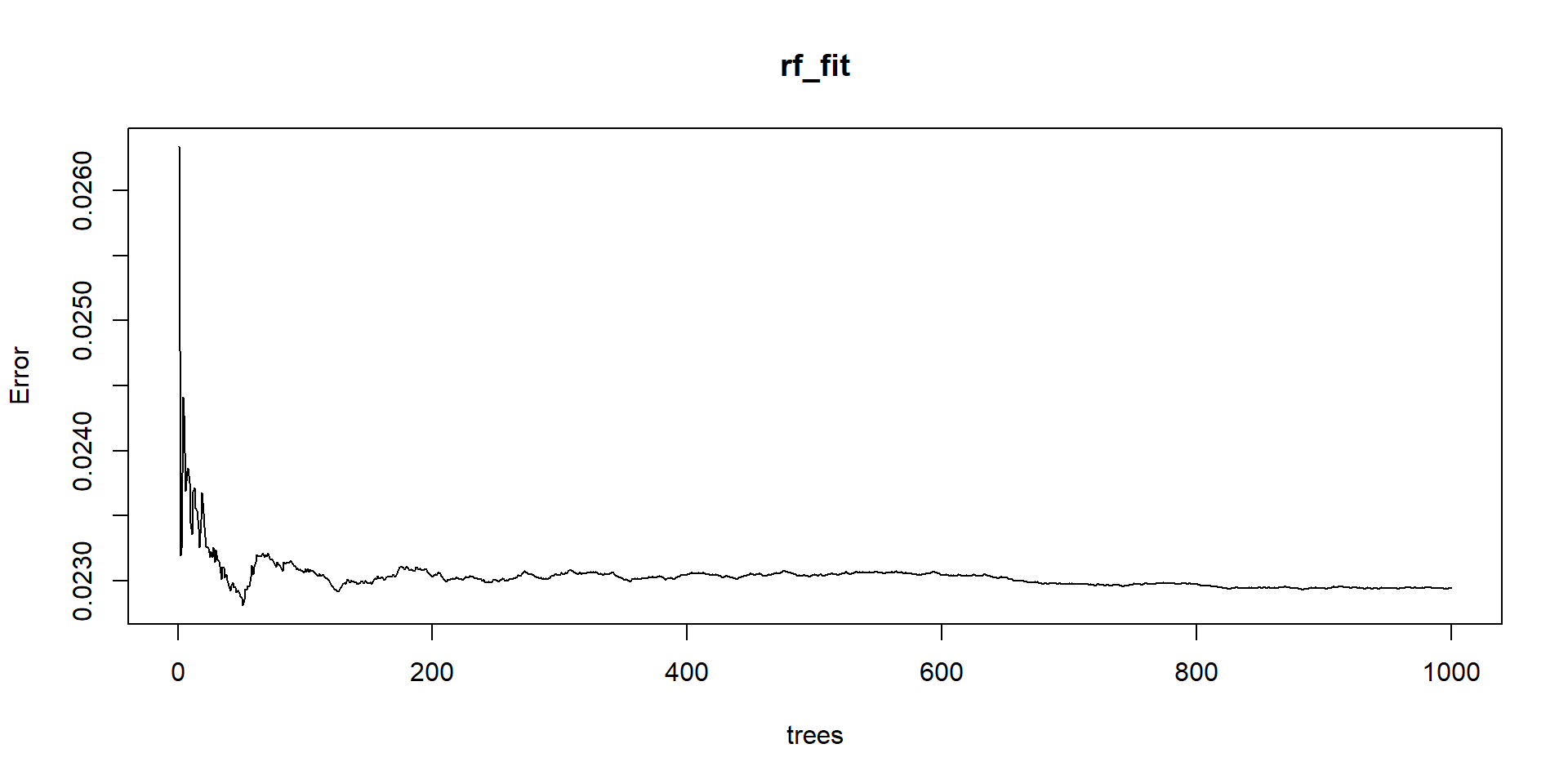
Call:
 randomForest(formula = default ~ ., data = Default, importance = T,      ntree = 1000) 
               Type of random forest: regression
                     Number of trees: 1000
No. of variables tried at each split: 1

          Mean of squared residuals: 0.02294122
                    % Var explained: 28.73

Error irreducible

plot(rf_fit)

Importancia de las variables

varImpPlot(rf_fit)

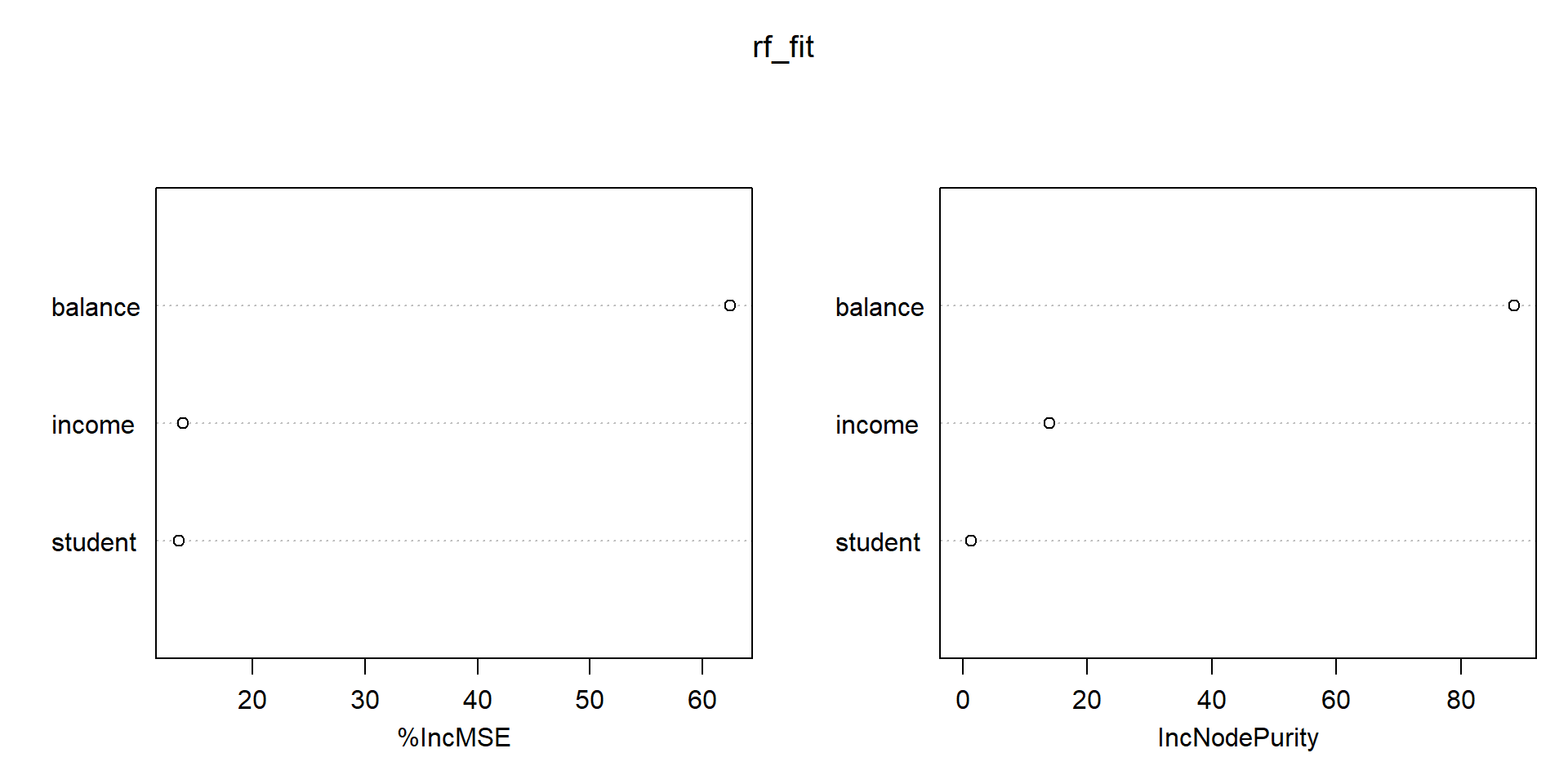
Bondades de Random Forest

• Los árboles son fáciles de interpretar.

• Pero se ajustan demasiado a los datos y son inestables.

Usamos Random Forest porque:

• Reduce la varianza sin aumentar el sesgo.

• Promedia el resultado de muchos árboles.

Un ensamble de predictores débiles y ruidosos de hecho puede ser un muy buen predictor si se combinan adecuadamente.

Pronóstico

Pronóstico de series de tiempo

Ahora pasamos a un nuevo conjunto de herramientas: el pronóstico.

• En tareas de pronóstico nos interesa predecir el comportamiento futuro de una variable en función de su comportamiento pasado.

• Asimismo, queremos brindar una métrica de la incertidumbre de la predicción.

Datos

Simularemos datos del número de incumplimientos de deuda en el tiempo.

pacman::p_load(tsibble, fable, feasts, urca)

default_ts <- tibble(
  date = yearmonth("2018-01") + 0:35,
  value = round(20 + 5 * sin(2 * pi * 1:36 / 12) + rnorm(36, 0, 2)),
  group = "n_defaults"
) |>
as_tsibble(index = date, key = group)

autoplot(default_ts)

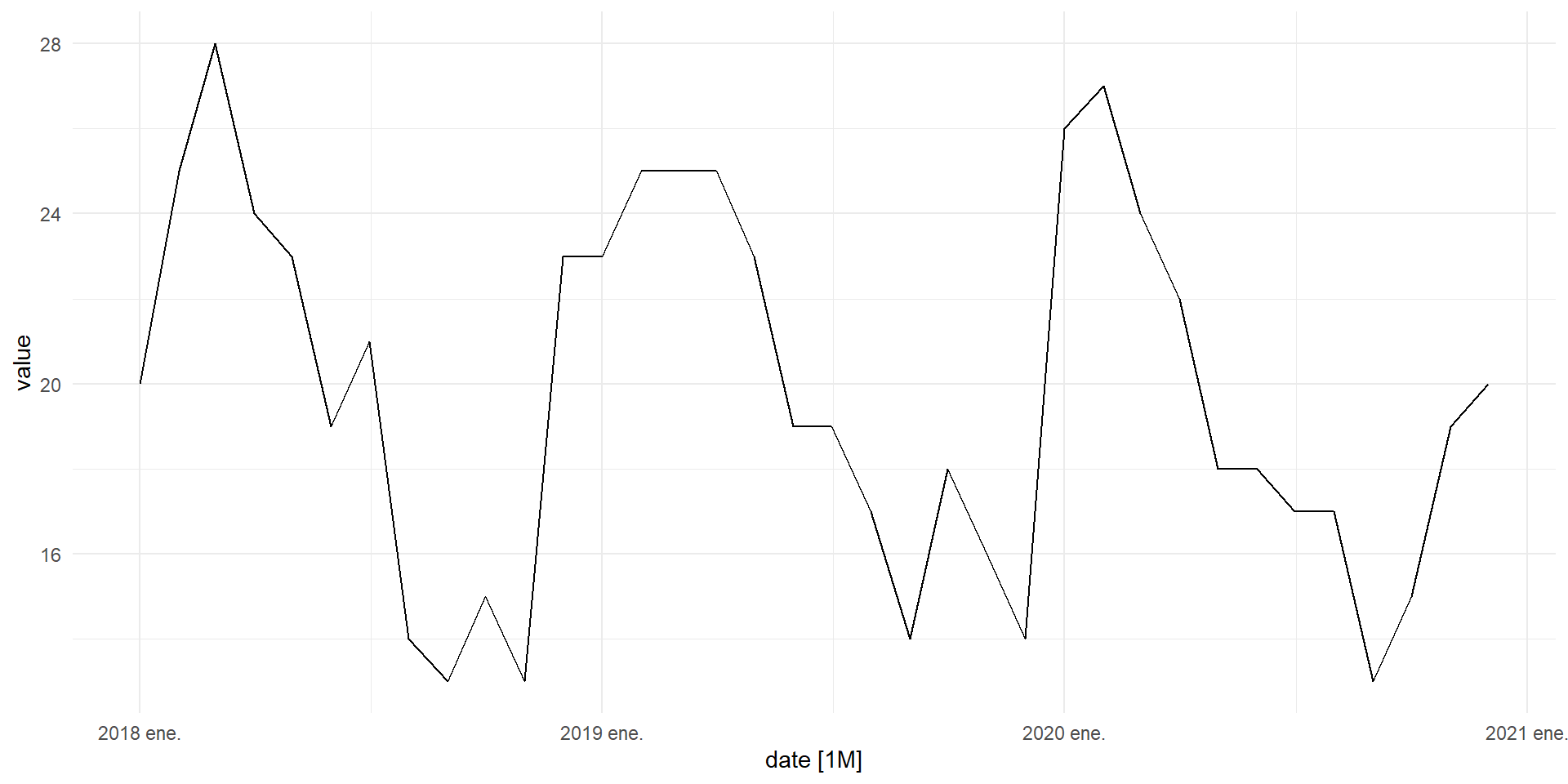
Pronósticos

model_fit <- default_ts |>
    model(
        arima = ARIMA(value),
        ets = ETS(value)
    )


forecast_fit <- model_fit |>
    forecast(h = "12 months")

autoplot(forecast_fit, default_ts) +
    facet_wrap(~.model) 

Referencias

Athey, Susan, y Guido W. Imbens. 2019. «Machine Learning Methods That Economists Should Know About». Annual Review of Economics 11 (1): 685-725. https://doi.org/10.1146/annurev-economics-080217-053433.

Hyndman, Rob J., y George Athanasopolous. 2021. Forecasting: Principles and Practice. Melbourne, Australia: OTexts. https://otexts.com/fpp3/.

James, Gareth, Daniela Witten, Trevor Hastie, y Robert Tibshirani. 2021. An Introduction to Statistical Learning: With Applications in R. 2nd ed. 2021 edition. New York NY: Springer. https://www.statlearning.com/.